INTRODUCTION
Si les paradigmes actuels de biomécanique Newtonienne sont vrais, alors, les forces calculées nécessaires à un grand-père pour soulever son petit enfant de trois ans devraient lui écraser la colonne ; attraper un poisson à la pêche à la mouche devrait arracher le bras du pêcheur à la ligne et les petits sésamoïdes seraient écrasés à chaque pas.
La vérité est que les grand-pères hissent leurs petits enfants et souvent les font sauter en l’air, les pêcheurs à la ligne attrapent des poissons dont le poids fait plus de dix newtons et qui peuvent se balancer au bout d’une ligne de plus de trois mètres et les footballers de 1000N parcourent les terrains sans écraser leurs minuscules et souples sésamoïdes. Les calculs sont bons ; le paradigme est faux et ne tient pas compte des réalités des fonctions biologiques.
Les structures biologiques sont de faibles consommatrices d’énergie, des systèmes ouverts, construits à base de matériaux visco-élastiques et souples qui se comportent de manière non-linéaire. Le calcul de charges, avec un corps appréhendé comme un levier de modèle linéaire Newtonien, créera des forces qui arracheront les muscles, écraseront les os et épuiseront les réserves énergétiques.
Fig. 1. Une tour de blocs est instable.
Selon la sagesse conventionnelle et les paradigmes actuels, la colonne et le squelette humain se comportent comme une colonne architecturale, une tour de blocs et supportent le poids du corps humain comme un pilier supportant un immeuble. 1 Cependant les colonnes architecturales s’orientent verticalement et fonctionnent seulement dans un champ gravitationnel (Schéma 1). Les colonnes, piliers et gratte-ciels sont rigides, immobiles, unidirectionnels et leur base est lourde afin de faire face aux forces d’écrasement. Ils résistent bien à la compression mais ont besoin de renforts lorsqu’ils sont pliés ou cisaillés. Étant soumises à des cisaillements internes, ce sont des structures hautes consommatrices en énergie.
Les lois rigides de la mécanique Newtonienne comme la loi de Hooke, la formule d’Euler, la loi cube au carré de Galilée et le ratio de Poisson gouvernent les colonnes conventionnelles. Si les systèmes biologiques se conformaient à ces lois, la colonne vertébrale humaine se plierait avec moins que le poids de la tête à son sommet 2 et les membres s’arracheraient au lever d’une canne à pêche à la mouche, tenue à la main. Les animaux plus grands qu’un lion se briseraient continuellement les os. Les dinosaures et mastodontes plus grands qu’un éléphant seraient écrasés sous leur propre poids. Les ptérodactyles n’auraient jamais pu voler. Si les vessies étaient gouvernées par les simples mécaniques Newtoniennes, elles exploseraient quand elles sont pleines, les utérus gravides se rompraient lors de fortes contractions, et à chaque battement cardiaque, les artères s’allongeraient suffisamment pour envahir le cerveau et le pousser hors du crâne 3 . Ce n’est pas que la mécanique Newtonienne soit fausse ; c’est le réseau de supposition qui est faux.
Un problème similaire apparaît en géométrie. La géométrie Euclidienne nous dit que des lignes parallèles ne se rencontrent jamais. Cependant, sur la surface de la terre, les lignes de longitude sont parallèles et pourtant elles se rejoignent aux Pôles Nord et Sud. La géométrie Euclidienne n’est pas fausse ; c’est juste que nous fabriquons un nouveau réseau de suppositions afin de décrire la géométrie de la terre. Il apparait ainsi que la géométrie Euclidienne est un cas particulier de géométrie où la courbure du plan est de zéro degré. La géométrie sphérique est une géométrie non Euclidienne. Il semble que la bio-architecture nécessite une pensée mécanique non-Newtonienne et non-Hookéenne, plus adaptable aux formes vivantes que les modèles Newtoniens et Hookéens. ...
INTRODUCTION
If the present paradigms of Newtonian based biomechanics hold true, then the calculated forces needed for a grandfather to lift his three year old grandchild would crush his spine, catching a fish at the end of a fly rod will tear the angler limb from limb, and the little sesamoid bones in our feet will crush with each step. The truth is that grandfathers hoist their grandchildren and often toss them in the air, anglers catch 10+ newton weight fish that may dangle from the end of a three-meter long fly rod and the 1000N footballer runs down the field without crushing his miniscule and soft sesamoid bones. The calculations are correct; the paradigm is faulty and ignores the realities of biologic functions. Biologic structures are low energy consuming, open systems, constructed with soft, viscoelastic materials that behave nonlinearly. Calculating loads with the body as a lever-beam, linear Newtonian model will create forces that rip muscle, crush bone and exhaust energy.

Fig. 1. A Tower of blocks is unstable.
According to conventional wisdom and present paradigms, the human spine and skeleton behaves like an architectural column, a tower of blocks, and supports the body weight as a pillar supports a building.1 However, architectural columns orient vertically and function only in a gravity field (Figure 1). Columns, pillars, and skyscrapers, are rigid, immobile, unidirectional and base-heavy to withstand crushing forces. They resist compression well but need reinforcement when stressed by bending moments and shear. Stressed by internal shear, they are high-energy consuming structures. Rigid Newtonian mechanical laws such as Hooke’s Law, Euler’s formula, Galileo’s square-cube law and Poisson’s ratio govern conventional columns. If biologic systems conformed to these laws, the human bony spine would bend with less than the weight of the head on top of it 2 and limbs will tear off with the leverage of a fly rod held in a hand. Animals larger than a lion would continually break their bones. Dinosaurs and mastodons larger than a present day elephant would have crushed under their own weight. Pterodactyls could never have flown. If governed by simple Newtonian mechanics, urinary bladders will burst when full, pregnant uteruses will rupture with strong contractions, and, with each heartbeat, arteries will lengthen enough to crowd the brain out of the skull.3 It’s not that Newtonian mechanics is wrong; it is that the set of assumptions is wrong. A similar problem arises in geometry. Euclidean geometry tells us that parallel lines never meet. However, on the surface of the earth, lines of longitude are parallel, yet they meet at the North and South Poles. Euclidean geometry is not wrong; it is just that we make a different set of assumptions in order to describe the geometry of the earth. It turns out that Euclidean geometry is a special case geometry where the curvature of the plane is zero degrees. Spherical geometry is non-Euclidean geometry. It appears that bioarchitecture requires non-Newtonian and non-Hookean mechanical thinking that are more adaptable to life forms than are Newtonian and Hookian models.
PRESENT SPINE MODELS
It is a teleological conceit that the human spine acts as a column. From gestation to age one, it never acts as a column. The human spine evolved from quadruped and lesser spines. Phylogenetic and ontogenetic development of the human spine was not in the form of a column, but as some form of a beam. It cannot be an ordinary beam, a rigid bar, but an extraordinary beam that is composed of semi-rigid body segments connected by flexible connective tissue elements that float the segments in space.4 In many postures, the adult human spine does not function as a column or even a simple beam. When the spine is horizontal, the sacrum is not a base of a column but the connecting element that ties the beam to the pelvic ring.
Even when upright, the vertebral blocks are not fixed by the weight of the load above, as they must be in an architectural pillar. The hallmark of a pillar is stability but the hallmark of a spine is flexibility and movement. Biologic structures are mobile, flexible hinged, low energy consuming, omni-directional structures that can function in a gravity free environment. The mechanical properties are non-Newtonian, non-Hookian and nonlinear. Columns need a stable base on which to rest. Therefore, columns are not useful as a model for fish or fowl or man in space. A post and beam is inadequate to model the neck of a flamingo, the tail of a monkey, the wing of a bat or the spine of a snake. Joints are slippery slopes and shear cannot exist in a frictionless joint. All forces must be normal to the surface to transmit loads. Post and beam modeling in biologic structures could only apply in a perfectly balanced, rigid hinged, immobile, upright spine with all joint surfaces normal to the force of gravity.
The spine can bend forward so a person can touch toes and bend backward almost equally well. It can twist and bend simultaneously. It can perform intricately controlled movements in space as done in gymnastics, dance, aquatic diving or basketball. With each breath, the interconnected vertebrae translate, some forward, some backward. While architectural columns bear loads from above the human spine can accept loads from any direction with arms and legs cantilevered out in any way. The hallmark of a pillar is stability but the hallmark of a spine is flexibility and movement. Movement of an articulated column, even along a horizontal, is more challenging than moving an upright Titan missile to its launch pad. ’S’ shaped curves can create intolerable loads and instability in a column, particularly if it is a thin, articulated column that has flexible, frictionless joints, as the spine does. The spine is flexible, mobile, and functionally independent of gravity and has property behavior inconsistent with an architectural column or beam.
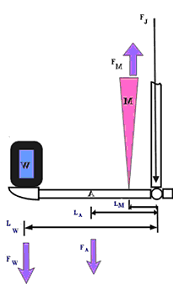
Fig. 2. The arm as a lever.
The free body diagram has been the reductionist approach to biomechanical modeling. Each segment is modeled in isolation. As noted by Ait-Haddou5 and others,6, 7 joints are spanned by tension elements that may span two or more segments. For example, the usual model for the elbow joint is the 90o-flexed elbow that supports a weight in its hand balanced by the biceps brachii muscle with the formula:
FA x LA + FW x LW - FM x LM = 0. FM is the weight of the load in the hand and FA is the weight of the arm8 (Figure 2).
However, the free body diagram poorly represents the true forces that must act in concert about any joint in the body. In the arm, the biceps is a two joint muscle and crosses the glenohumeral joint in addition to the elbow joint. As the biceps crosses the glenohumeral joint, that creates a moment at the shoulder. The glenohumeral joint is stabilized be antagonist muscles, such as the triceps, which is a muscle that extends the elbow and it must then enter into a feedback loop with the biceps. Holding a weight in the hand requires the use of the wrist flexors and finger flexors. They also cross the elbow joint and will create moments that need to be counterbalanced with the triceps, and so on. The glenohumeral joint connects to the axial skeleton through the scapula, which suspends from the chest wall by muscles that must also enter into the feedback loop. It is clear that there are no sharply defined segment boundaries. In the scapulo-thoracic complex, no rigid structure that can act as a fulcrum as there is no bone-on-bone contact. Without a fulcrum, there is no lever. Any moments passed from arm to axial skeleton is only accomplished through the tension of muscles. You can only pull with a muscle, it cannot act as a rigid lever.
Loads calculated when using free body analysis frequently exceed known tissue capabilities. In the usual free body analysis of the hip, the calculated loads are seven to ten times body weight. With a 1000 N footballer running down the field the calculated load on the articular cartilage will be in the range of 12-15 MPa and more. It is a poorly kept secret that articular cartilage is incapable of sustaining the calculated loads on it without considerable help.9 The erectores spinae muscles can only withstand loads of 2000-4000N. During weight lifting, using free body analysis, the loads on the erectores spinae can exceed 16000N.10 Clearly, free body analysis misrepresents the true picture. Free body diagrams are inadequate and even deceiving, approximations of the true forces at any one joint.
ALTERNATIVE MODELS
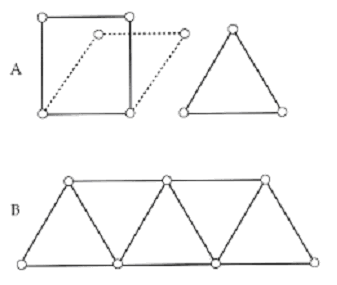
Fig. 3. A. Square frames are unstable and create torque at the joints. Triangular frames are inherently stable. B. A simple, planar truss.
There are alternative models to the column that may be more appropriate for spinal models of all species, not just bipeds. D’Arcy Thompson11 and, latter, Gordon12, use truss models. A truss is fully triangulated and is inherently stable and independent of gravity. Trusses have flexible, even frictionless, hinges with zero moments about the joint. Loads applied at any point distribute about the truss, as tension or compression. There are no levers within a truss. Only trusses are inherently stable with freely moving hinges. Vertebrates are stable, with flexible joints and, therefore, constructed as trusses if they are to stand upright. Thompson compared a dinosaur to a trestle bridge with the bones as the compression elements and the muscles and ligaments as the tension members. In a truss, the loads distribute through the system, as tension and compression only and the joints can be pin hinges, as there are no moments generated (Figure 3).
In two dimensions, we can start with a single triangle, the basic truss, and add more triangles. Three dimensional, or space trusses, are some combination or permutation of the three regular polyhedrons that are fully triangulated, the tetrahedron with four triangulated faces, the octahedron with eight and icosahedron with twenty (Figure 4).
The icosahedron has some distinct advantages in biologic modeling. It has the largest volume for surface area, an economy of resources, and has the ability to be close packed to fill space.
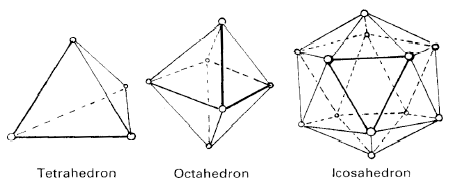
Fig. 4. Three dimensional, fully triangulated, regular polygon trusses. Only fully triangulated polygons are stable when the joints are flexible.
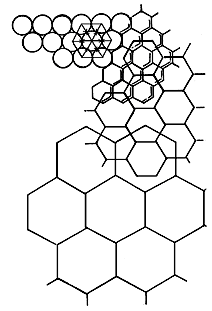
Fig. 5. Hexagonal close-packing. Self-generating tessellation of a plane.
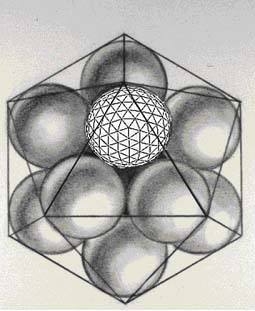
Fig. 6. Close packing of icosahedral geodesics about a central space. Self-generating tessellation in three-dimensional space.



