Equilibriste ?
Quand un ostéopathe pose ses mains sur un corps, il touche, teste, perçoit, exécute des gestes qui modifient le corps du patient vers un équilibre que l’on espère meilleur puis il lâche le corps pour que dans son autonomie le patient aille mieux : dans son corps, dans ses émotions, dans son esprit, dans son énergie, dans son interaction sociale.
Cela pourrait être suffisant, mais dans un monde numérique et matérialiste, il convient de justifier qu’il s’est bien passé quelque chose et dès que l’on s’éloigne des manipulations structurelles pour rentrer dans le fonctionnel, le fluidique ou que sais-je encore, il devient de plus en plus difficile de justifier chiffres à l’appui que ce qui s’est passé est bien réel et non pas issu des sensations d’un cerveau au mieux abusé par lui-même au pire manipulateur.
Aussi la tentation de recadrer l’ostéopathie dans le structurel musculo-squelettique est-elle de plus en plus forte et l’exclusion du crânien, du viscéral et autres dérives qui ne tiennent pas compte de la réalité quantitative est de plus en plus d’actualité.
La tentation pour l’ostéopathe de s’en sortir simplement en disant que l’ostéopathie, la santé et la vie sont des choses si complexes que l’on ne pourra sans doute pas les réduire à quelques séries de chiffres, en tous cas pas avant longtemps, est aussi très forte. En tous cas, tout qualitatif que ce soit, nous pouvons nous permettre de dire que nous avons expérimenté avec assiduité pendant des années et que cela semble très bien fonctionner, alors nous aimerions simplement que l’on nous laisse travailler à notre guise !
Mais justement puisqu’il est question de preuves, de chiffres, de réalité objective, allons faire un petit tour du côté des mathématiques qui comme toujours peuvent nous en dire long sur notre monde tel qu’il est appréhendé.
Naturel ou réel ?
Quand il s’est agi de compter pour procéder à des échanges, l’homme a d’abord procédé comme sait le faire le corbeau qui arrive à savoir combien il y a de personnes dans une pièce de manière globale et intuitive et ce jusqu’à une quantité que nous appellerions 7 dans notre façon actuelle de compter. Puis l’homo numéricus est arrivé assez facilement aux nombres naturels (1 arbre, deux personnes, trois chevaux, 50 kilos …) ce qui nous amène à l’ensemble des nombres Naturels (N). Très vite on a fait des opérations sur ces nombres : deux chevaux dans un pré et un dans l’autre font trois chevaux. Addition, soustraction puis multiplication et division sont apparues mais il a fallu quelques milliers d’années pour que le Zéro apparaisse c’est-à-dire un nombre qui représente une non quantité.
Imaginer une quantité négative a demandé aussi du temps (il me manque trois pommes pour finir de remplir mon panier) et cela nous a amené à imaginer un ensemble plus grand que N que l’on a noté Z des nombres relatifs qui contient des nombres positifs et des nombres négatifs. Puis l’usage de la division (partager le pré de la rivière en trois pour chacun de mes fils) a apporté son lot de complication en obligeant à imaginer des portions d’entiers (un gâteau partagé en deux fait 0.5 gâteau un demi (1/2) gâteau) ce qui nous fait considérer deux ensembles plus grands que Z :
– Les nombres décimaux ceux qui ont un nombre fini de décimales (0,456 ou 6/15) (D)
– Les nombres rationnels contiennent les précédents et ceux qui ont un nombre de décimales infinies mais qui répètent toujours la même structure périodique : 1/3 ; 0.898989 (Q)
– Et puis il y a les autres, les irrationnels, ceux qui ont été trouvés au détour des équations et dont personne ne comprend la raison d’exister mais ne peut qu’admettre. Il y a là un bestiaire de chiffres tels que φ (Phi) le nombre d’or, π (pi), notre fameux 3.1415 etc., le e du logarithme naturel, √2 …tous avec un nombre infini de décimal qui ne se répètent jamais, des nombres que l’on retrouve régulièrement au détour de problèmes variés, bornes incompréhensibles et inévitables de notre univers … et l’on termine alors avec eux sur l’ensemble des nombres réels (R).
Jusque-là, si l’on excepte les quelques irrationnels un peu agaçants, tout est convenu, logique et simple …. L’entendement humain est ménagé et tout va bien.
Mais le problème avec les mathématiciens, c’est qu’ils ont tendance à prendre les nombres comme des jouets et à passer des nuits entières à résoudre des trucs qui ne servent apparemment à rien quitte à inventer des pirouettes mentales.
Des Complexes ?
C ’est ainsi qu’au XVIe siècle déjà Cardan (piquant l’idée de Tartaglia…) écrit que pour résoudre l’équation x(10-x) = 40, il convient d’avoir recours à la racine carré d’un nombre négatif. Quand pourtant un nombre fut’ il négatif multiplié par lui-même donne toujours un nombre positif ce qui rend impossible l’existence de la racine carrée d’un nombre négatif mais (5-√-15) est bel et bien une solution de l’équation ci-dessus. Alors s’en est suivi une longue période où des mathématiciens ont refusé de jouer avec des nombres qui n’existaient pas et d’autres ont décrété qu’irréel ou pas ces nombres pouvaient servir et qu’ils s’en serviraient ! Ils ont quand même un peu biaisé en introduisant un nombre i (imaginaire) qui valait √-1 et la solution précédente devenait 5-15i, cachant ainsi la honteuse impossibilité mais en ouvrant la voie à la résolution des équations de troisième et quatrième degré puis à la création des nombres complexes (C) qui seront à l’avenir écrits :
– Nb complexe = nb réel + nb’ réel*i (nb imaginaire) et l’histoire continue ainsi avec un malaise sévère des mathématiciens qui voient là un artifice non réel mais pourtant si facile !
Pire que cela, alors que les nombres réels se suivent sur une ligne, les nombres complexes donnent une deuxième dimension aux nombres qu’on peut retraduire sur un plan et résoudre ainsi des problèmes géométriques ardus. Ils interviennent dans le calcul d’intégrales, dans la résolution des fractales, dans les surfaces de Riemann (on revient aux univers non euclidiens !).
| Les fractals sont une composante de nos corps (arborescence des artères du poumon par exemple) ici un fractale de Mandelbrot |
Mais le ver est dans le fruit quand on découvre qu’il peuvent déborder les maths et rentrer en physique. En optique en particulier sur la problématique de la lumière polarisée ils sont incontournables, et enfin pour unir le magnétisme et l’électricité il n’y a qu’eux !
Et le pompon c’est que partant sur la lancée des nombres à deux dimensions les physiciens ont utilisé des nombres à 4 dimensions ou à 8 (Quaternions et Octonions) appelés hypercomplexes et …. Avec eux on peut résoudre en physique quantique la problématique des particules en intégrant le Spin (mouvement rotatoire de valeur discrète et caractéristique de chaque particule). On notera d’ailleurs que le spin du photon (plutôt hélicité d’ailleurs… cela me rappelle quelque chose) est important dans les problèmes de polarisation de la lumière…
Il est ainsi très étonnant de constater que nos collègues mathématiciens et physiciens pour décrire la complexe réalité dans laquelle nous baignons aient eu besoin d’un nombre imaginaire √-1 qui ne peut exister, mais que cet outil ait fini par tellement les interpeller qu’ils n’ont pas pu s’en passer et finir par admettre son existence.
Conclusions ...
Que tirer de ce petit tour de l’usage des nombres pour quantifier ce qui nous entoure ?
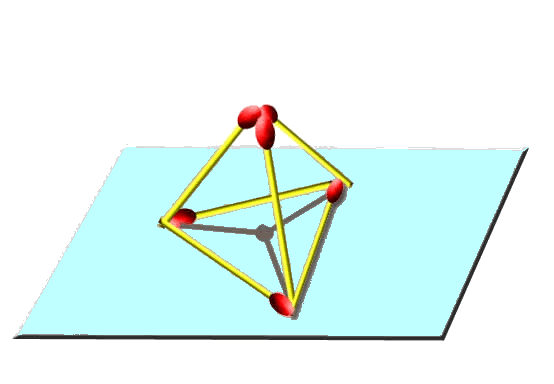
– Pour décrire le monde physique il a fallu ajouter aux nombres des dimensions supplémentaires et aller jusqu’à un monde à 4 ou 8 dimensions, c’est la même chose que pour résoudre le petit exercice suivant : voici 6 allumettes, faites 4 triangles équilatéraux. Ce problème ne se résout qu’en sortant du plan d’une feuille.
– Pour décrire le monde physique il a fallu inventer un nombre qui n’existe pas et accepter qu’il puisse avoir une utilité et une action sur le réel, ce nombre c’est i, soit le nombre imaginaire. Pour décrire la complexité du monde, il convient donc d’utiliser des nombres réels et avoir de l’imagination, on réintroduit l’esprit, l’intuition dans le quotidien pour comprendre la complexité des choses, c’est ce qui est littéralement écrit dans la construction des nombres complexes : Nb complexe = nb réel + nb’ réel*i (nb imaginaire).
Et depuis que Göedel est passé par là avec ses théorèmes d’indécidabilité et d’incomplétude qui nous disent qu’un ensemble ne peut être démontré qu’à partir de quelque chose d’extérieur à lui, il est bien normal que l’ensemble des réels (R) puisse être justifié par quelque chose d’étranger à lui même et i, nombre hors de la réalité usuelle joue très bien ce rôle !
Ce qui a été fait en mathématique puis en physique depuis plus de 400 ans maintenant, c’est-à-dire accepter qu’un outil iconoclaste puisse avoir une utilité pour décrire le monde devrait maintenant être accepté en biologie et en médecine.
Ainsi la complexité du vivant mériterait que la médecine académique avec sa description dichotomique et chimique du vivant s’adjoigne une deuxième dimension dans le soin : toutes les médecines énergétiques et intuitives qui seraient alors le deuxième terme décrivant l’état de santé du patient.
En effet, les fractals sont inscrits dans nos corps, l’électromagnétisme nous accompagnent, les Biophotons de fritz Pop résonnent avec la polarisation et les nombres complexes, avec la torsion physiologique le spin des particules est là, notre cerveau droit fait office de (i) dans son fonctionnement, etc.
Introduire ces données pourrait s’écrire dans une équation similaire à celle qui régit les nombres complexes :
– S = MC + MC*MI, où S est l’état de santé global et complexe du patient, MC est ce qu’en pense la médecine académique et matérialiste ( y compris l’ostéopathie mécaniste) et MI, ce qu’en pense toute médecine intuitive (ostéopathie, acupuncture, médecine ayurvédique, chamanisme, etc.) raccrochée aux trois dimensions de ce monde par un terme modérateur.
Mais cela nécessite d’accepter MI comme on a accepté le nombre imaginaire (i) : un outil improbable, mais tellement utile et indispensable pour décrire la fragilité d’un état de santé. MI l’ensemble extérieur qui valide MC d’après les théorèmes de Gödel).
Je crois que le jour où nos amis médecins et biologistes accepteront cela simplement on pourra enfin faire du bon travail ensemble et faire une recherche digne de ce nom dans laquelle l’ensemble S des états de santé permettra de résoudre élégamment les problématiques de nos patients et où l’addition d’une dimension au monde de la santé rendra logique ce qui s’y passe.
Tant que ce travail n’est pas fait et accepté de tous, MC et MI sont des paradigmes incommensuraux, c’est-à-dire qui qu’ils décrivent le statut de deux paradigmes successifs appliqués à une même science et dont la comparaison est impossible, en raison de différences fondamentales dans leurs structures et les schèmes de pensée qu’ils introduisent… cela est fort dommage.
Merci Monsieur Tartaglia d’avoir oser imaginer l’inimaginable, nous vous devons beaucoup ! A nous de nous montrer digne en mettant en action l’ensemble S et pourquoi pas un jour un équivalent des Quaternions ou Octonions : raisonner non plus sur 1 dimension, ou bien 2, mais 4 ou 8 !!
Bibliographie :
http://www.cerveauetpsycho.fr/ewb_pages/a/article-les-corbeaux-sont-ils-intelligents-20006.php
http://soocurious.com/fr/dans-le-remarquable-cerveau-du-corbeau-loiseau-capable-de-resoudre-des-puzzles-complexes-en-8-etapes/
– https://fr.wikipedia.org/wiki/Incommensurabilit%C3%A9
– https://fr.wikipedia.org/wiki/Ensemble_de_nombres
– https://fr.wikipedia.org/wiki/Histoire_des_nombres_complexes
– https://fr.wikipedia.org/wiki/Nombre_hypercomplexe
– https://fr.wikipedia.org/wiki/Spin
– https://fr.wikipedia.org/wiki/Quaternion
– https://fr.wikipedia.org/wiki/Incommensurabilit%C3%A9
– https://fr.wikipedia.org/wiki/Nombre_irrationnel